Can distillation training allow for faster architecture search?

Deep learning model architectures can process arbitrary data. Even models developed and usually used with a certain type of data can process others well. Transformers were invented for NLP and now they’re used in almost every conceivable seq2seq task.

This less true for brains. Brains have large areas dedicated to certain types of data. Some of these areas can be repurposed for other types of data, but presumably they function best when processing what they evolved to process.

Although AI models can be thought of as ‘evolving’ in training, it’s distinct from biological evolution in an important way: There are way more constraints for AI than for biology. The equivalent of biological evolution in AI would be the raw bits or instructions mutating, but in reality it’s just the weights that change.

Thus, the current SOTA architectures are basically just what (extremely smart) humans have stumbled on so far that works well enough. Models that target certain data are not really shaped by the data in any meaningful way, like your visual cortex was shaped by hundreds of millions of years of information coming from your eyes.

Current models can match human performance in an ever-growing array of tasks, but they need way more data than humans do.

Thus, there’s a clear potential in trying to train AI in a way more similar to how the brain evolved, and hope that it makes AI better at things that brains are good at. [1] [1] This is very handwavy, but not any more handwavy than most other justifications in AI, where theory still lags years behind empiricism.

There are some people starting to try this way of training that puts much more flexibility in the hands of the optimization algorithm. It’s not an easy problem. The search space gets way, way, way larger if you let the architecture grow as well as the weights, and most architectures won’t work very well or at all. This is why architectures exploration has just been smart humans with some grid search up to now: there are just too many options and no good way to eliminate most of them [2] [2] Even when you already eliminated most of them using something like directed evolution to modify a known good architecture, instead of starting from nothing. without training the architecture and seeing how it does, which can take a lot of compute.

I’d like to explore directed architecture evolution in the future. But first, I tried to speed up a core part of it: training and evaluating new architectures.

To do this, I used the MNIST dataset and distillation. The idea was to see if distillation can allow a given architecture to be evaluated faster, because each training step has a lot more data: Instead of a one-hot vector (which when there’s 10 classes is log2(10) = 3.32 bits), you get a full distribution to train on, generated by the teacher model.

From what I’ve seen, most knowledge distillation research has focused on creating smaller models that do a task mostly as well as a larger model, instead of using distillation to evaluate a model’s training performance, with the teacher being around the same size.

So, I went ahead and trained a bunch of models with a grid search - code here - to look at the performance of distillation (only) vs cross entropy loss (only) from the labels. For now, I kept the architecture constant and pretty bog standard for MNIST: 3 convolutional layers (32, 64, 128 channels), 2x2 max pooling for each, then 2 fully connected ReLU neural nets, with 50% dropout.

I swept the learning rate, temperature, and fraction of the full dataset to train on (for 1 epoch). For the actual distillation implementation, I used the same teacher model for all examined student models, and trained it on the full dataset (training fraction = 1.0, again for 1 epoch). Then for each hyperparameter combination (selected 5 of each, so 125 different combinations) I trained a model using only distillation from the teacher model with a Kullback Leibler divergence loss, and a model using only the labels using cross entropy loss. Each model’s training was repeated 5 times, and the final loss averaged between them. Results are below. Note that each point is the average of all of the hyperparameter combinations that had that hyperparameter value present (I wanted to make it easy to visualize while also showing the broad trends across the experiment, without excluding any data). I also visualized this data in a 3D heatmap but it didn’t really add much.

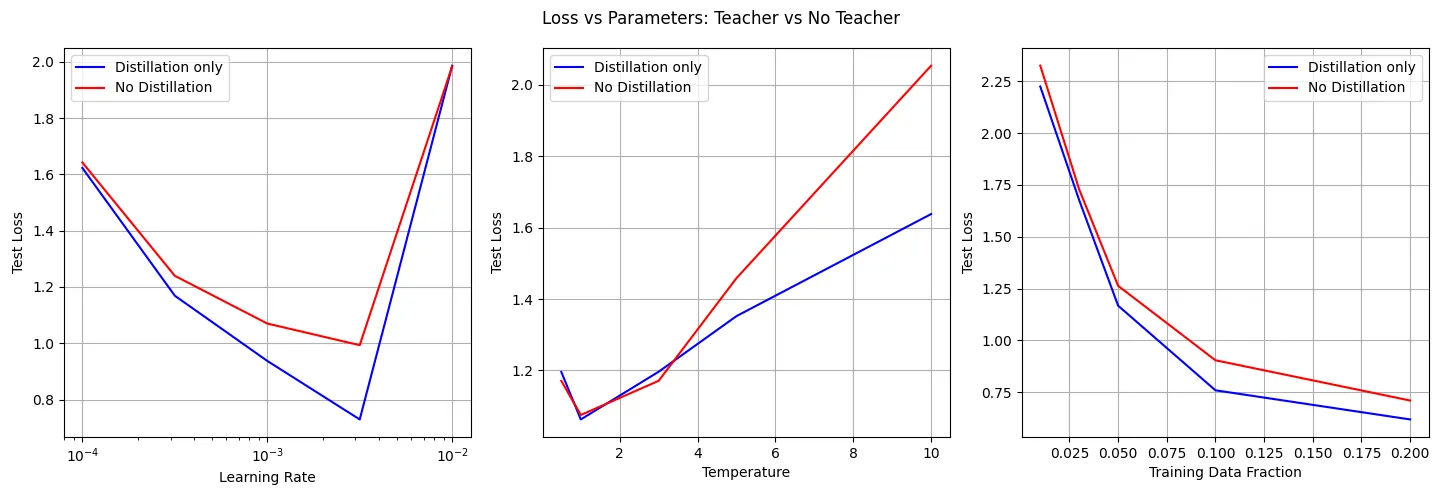
So, in the low-data regime, distillation does seem to teach models slightly faster. The left plot is the most important: It shows that just before the learning rate gets too high for stable learning, distillation significantly outperforms the alternative.

I re-ran the experiment, narrowing in on the interesting areas in the first and second plots:

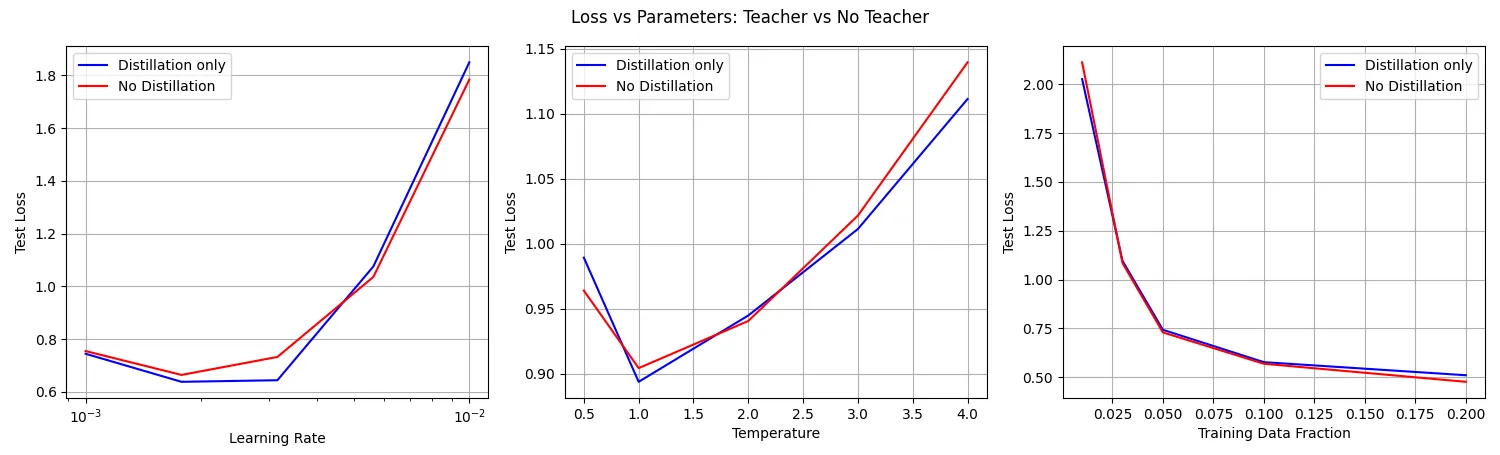
The result on the left shows that, for this experiment’s hyperparameters, around 0.0011 learning rate gives the best performance for the distilled training.

The middle result confused me though. I expected the peak performance to be at the temperature that the teacher model was trained at (3). I ran another test, now looking at both accuracy and loss, and training a new teacher model at each temperature:

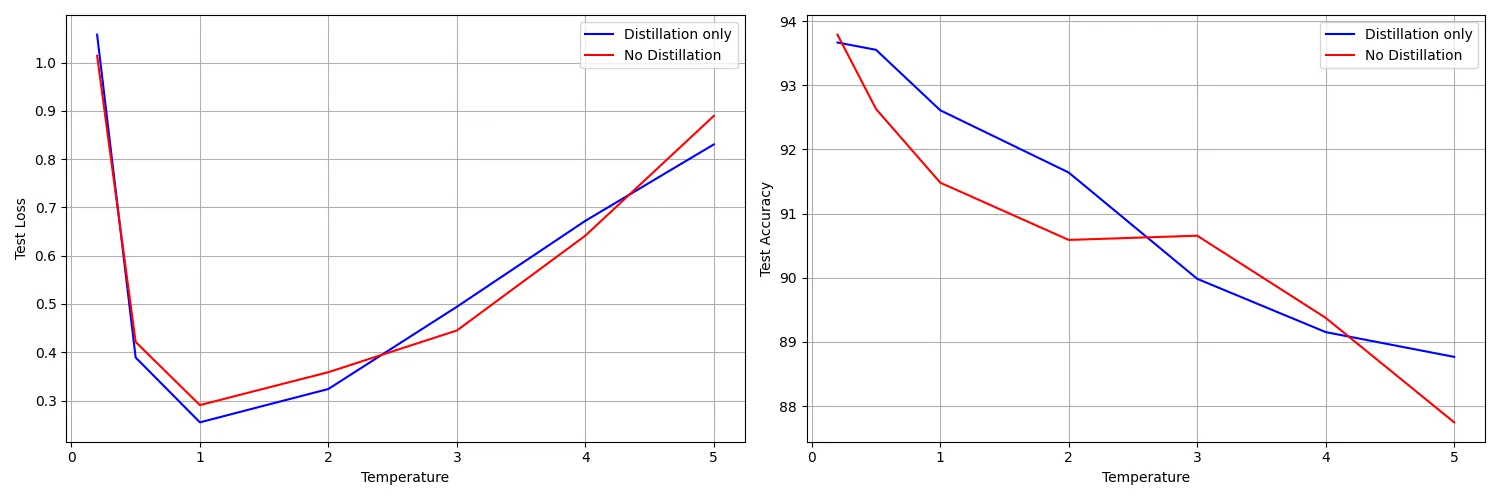
So, it seems like the most effective temperature, for this dataset and other hyperparameters, is actually as low as possible. Some of the first distillation research (By none other than Geoff Hinton!) found that a temperature of 2.5 to 4 worked best for nets with “300 or more” neurons. In this experiment, both of the FC layers have way more than 300 neurons.

It could be that, because of the small amount of training data (the above experiment used train_frac = 0.05), there isn’t enough ambiguous data seen for temperature to have much of an effect. Higher temperatures should help the most for ambiguous data - at temp=0, if the logit predictions are 51% “1” and 49% “7”, the actual output will be 100% “1”, so any information besides the top pick is lost. It might also be that MNIST isn’t a very ambiguous dataset in general. It’s also not clear to me why, below 1, loss spikes but accuracy continues to improve closer to 0. This implies that, the lower the temperature is, the top prediction is more likely to be correct but the output distribution is less similar to the one-hot label. I would expect the output distribution to be more similar to the one-hot label at lower temperatures, so I’m not sure what’s going on here - more investigation is needed.

Conclusion: KL-div distillation is a moderate improvement over labels + cross-entropy, in the low-data conditions of the experiment. It should give a corresponding moderate performance improvement in architecture search, especially at higher learning rates. More investigation is needed to be able to say how well performance in this experiment’s low-data regime correlates with well-trained model performance, but it’s at least some signal, and with distillation you can train the models a little bit further down the loss curve for the same training steps.

(Note that I’m fairly new to ML and don’t expect any of this to be novel, it’s just fun. :) If there’s any mistakes please let me know!)